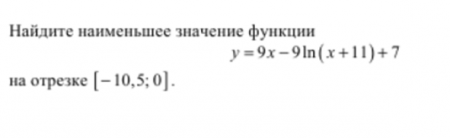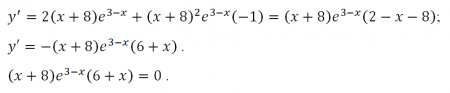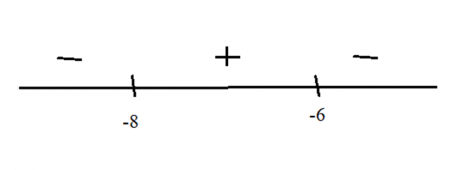Как решать ЕГЭ по математике

Готовимся к ЕГЭ по математике: решаем задачи с использованием производной

ЕГЭ, единый государственный экзамен, сейчас является обязательным условием поступления в ВУЗ для выпускников. Но даже если ученик не планирует поступать в университет, он для получения аттестатаобязательно должен сдать ЕГЭ по 2-м предметам: математике и русскому языку.

В будущем Министерство просвещения планирует добавить к обязательным экзамены по обществознанию и иностранному языку. В этом году кардинальных изменений не будет.

Экзамен по математике может бытьбазового или профильного уровня. Раньше можно было этот экзамен сдавать два раза:профильный и, для подстраховки, базовый. Сейчас можно выбрать только один уровень.

Задачи по математике достаточно типовые, поэтому подготовиться к ЕГЭ не очень сложно.

Важно! Нужно внимательно читать условия задач, поскольку, если задача решен, но ответ записан неправильно или не соответствует вопросу, задача не будет засчитана.

Рассмотрим решение задач профильного уровня, которые требуют знания темы производной функции.

Задачи на смысл производной

Производная y¢функции y(x) определяется следующим образом:

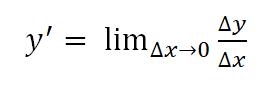
при условии, что этот предел существует.

В области существования производнойсправедливы следующие ее свойства:

1)      на интервалах возрастания функции производная положительна;

2)      на интервалах убывания функции производная отрицательна;

3)      в точках экстремума (максимума или минимума) функции производная равна нулю.

Для дифференцируемой функции для свойств 1) и 2) справедливы и обратные утверждения. Утверждение, обратное 3), неверно. Поэтому точки, в которых производная функции равна 0, часто называют подозрительными на экстремум.

Геометрический смысл производной в точке: значение производной в точке x₀равно тангенсу угла наклона касательной к графику функции в данной точке. Таким образом, по величине этого угла можно определитьзнак производной: она отрицательна, если угол больше 90°, но меньше 180°, иположительна, если угол больше 0, но меньше 90°.

Рассмотрим несколько примеров решения задач. В скобках указан номер задачи в демо варианте.

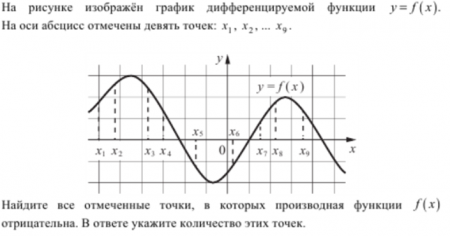
Задача 1(7)

Рис.1. Условие задачи 1

Согласно свойству 2) производная будет отрицательна в точках, которые расположены внутри интервалов убывания функции. На рис. 2 эти интервалы показаны красным цветом.

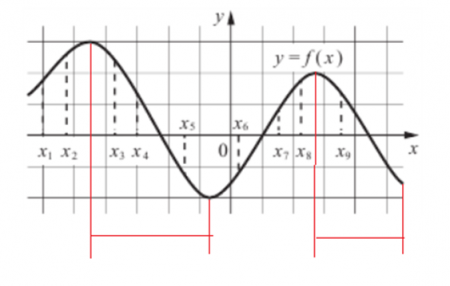
Рис.2. Интервалы убывания функции

Внутри выделенных интервалов находятся следующие точки: x₃, x₄,x₅ иx₉. Количество точек равно 4. Это и будет ответом задачи.

Задача 2(7)

Красным цветом показаны дополнительные построения в исходном рисунке.

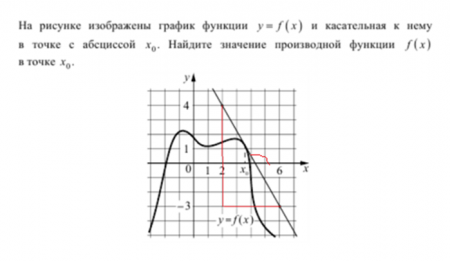
Рис.3. Условие задачи 2

Решение задачи определяется геометрическим смыслом производной. Угол (показан красной дугой) лежит в интервале (90°; 180°).Следовательно его тангенс (как и значение производной в точке x₀) будет отрицательным.

Вычислим тангенс смежного острого угла. Значение этого тангенса будет отличаться от искомого только знаком. Выберем треугольник, катеты которого выражаются целыми числами (показаны на рисунке красными линиями). Тангенс (как отношение противолежащего катета к прилежащему) равен 7/4 = 1,75. Следовательно, значение производной в точке x₀равно, с учетом знака,-1,75.

Задачи на экстремум

Как уже упоминалось, в точке экстремума производная дифференцируемой функции обращается в ноль. Возможны три случая:

• если в точке производная меняет знак с + на - , т.е. функция возрастает, а потом начинает убывать, экстремум в точке является максимумом;
• если в точке производная меняет знак с -на + , т.е. функция убывает, а потом начинаетвозрастать, экстремум в точке является минимумом;
• если знак производной не изменяется, экстремума в точке нет.

Рассмотрим несколько задач на вычисление экстремума.

Рис.4. Условие задачи 3

Находим производную заданной функции, используя правило вычисления производной суммы функций и таблицу производных элементарных функций:

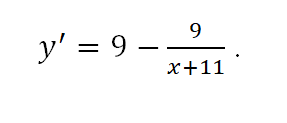
Находим точки, подозрительные на экстремум, приравнивая производную нулю. Получаем уравнение:

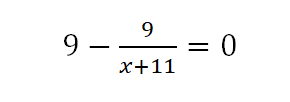
Решая это уравнение, получаем:

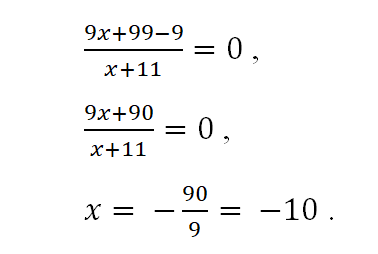
Дробь 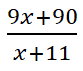 на отрезке [-10,5; 0] отрицательна приx< -10 и положительна при x> -10. Следовательно,на этом отрезке найденная точка является точкой минимума функции.

Чтобы найти минимальное значение функции на рассматриваемом отрезке, подставляем значение x = -10 в выражение функции:

y_min = 9×(-10) – 9×ln(-10 + 11) + 7 = -83 .

Задача 4(12)

Рис.5. Условие задачи 4

По аналогии с предыдущей задачей, находим производнуюфункции (в данном случае используя еще правило вычисления производной сложной функции) и точки, подозрительные на экстремум.

Поскольку экспонента не обращается в нуль, полученное уравнение можно записать в виде:

(x+ 8)(x + 6) = 0.

Это уравнение имеет решения: x₁ = -6, x₂ = -8.

На рис. 6 показаны интервалы знакопостоянства производной функции, с учетом знака - в выражении для y¢.

Рис.6. Изменение знака производной функции

Следовательно, в точке -6 функция имеет максимум, а в точке -8 – минимум.Учитывая условие задачи, записываем в ответе значение -6.

Следует отметить, что задачи на нахождение экстремума более разнообразны, чем те, которые рассмотрены в примерах. В частности, следует учитывать, что экстремум может достигаться в точках, где функция не является дифференцируемой, т.е. не имеет производной. Примером такой функции является , которая имеет минимум в точке x = 0, но не имеет в этой точке производной.

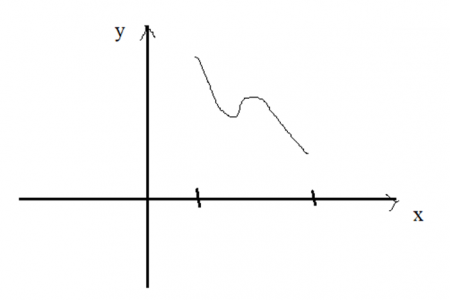
Также на отрезке экстремум может достигаться не только в точках внутри отрезка, но и на его концах. Пример такой функции схематично показан на рис. 7.

Рис.7. Пример функции, экстремумы которой достигаются на концах отрезка

Для качественной подготовки к экзамену, особенно, профильного уровня, нужно стараться решать как можно больше разнообразных задач различного уровня сложности, не ограничиваясь демонстрационными вариантами.